STANDARD DEVIATION along with AN EXAMPLE
STANDARD DEVIATION :
Standard deviation for every grade of concrete shall be calculate separately. Because the value of standard deviation various based on the material used and batch mix. Based on the number of trials and based on the Indian standards.
CALCULATION:
Hera this table showing that the calculation of standard deviation for a Set of 30 Concrete Cube Test Results.
Average Strength, μ = 1265/30 = 42.167 MPa
Standard deviation = √[489.9/ (n-1)] = √(489.9/29) = 4.11 MPa
Where, n = Total number of samples
Coefficient of Variation = (Standard deviation/Average strength)*100
= (4.11/42.167)*100
= 9.79
standard deviation based on test strength of sample:
1.
Number of test results of samples - The
total number of test strength of samples required to constitute an acceptable
record for calculation of standard deviation shall be not less than 30, Attempts should be made to obtain from the 30 samples of motor cubes or concrete cubes
(taken from site or laboratory) based on you requirement, as early as possible. When a mix is used for the first time.
2. In
case of significant changes in concrete – when ever significant changes are made in the production
of cement concrete batches (for example changes in the materials used, based on
the mix Proportioning and equipment or technical control), the standard
deviation value shall be calculated separately for such batches of concrete.
3. Standard
deviation to be brought up-to date - The calculation of the
standard
Deviation
values shall be brought up-to-date after every change of mix proportioning.
Assumed standard deviation:
When
where sufficient test results for a particular grade of concrete are not
available, then the value of standard deviation given in Table1 may be assumed
for the proportioning of mix in the first instance. As soon as the results of
samples are available, actual calculated standard deviation shall be used and
the mix proportioned properly. However, when adequate past records for a
similar grade exist and justify to the designer
a value of standard deviation different from that shown in Table 1, it shall be
permissible to use that value.
Table 1 Assumed Standard Deviation
(Clauses 3.2.1.2,
A-3
and B-3)
Sl.No
|
Grade of Concrete
|
Characteristic compressive
strength (N/mm2)
|
Assumed standard deviation (N/mm2)
|
1.
|
M10
|
10
|
3.5
|
2.
|
M15
|
15
|
|
3.
|
M20
|
20
|
4.0
|
4.
|
M25
|
25
|
|
5.
|
M30
|
30
|
6.0
|
6.
|
M35
|
35
|
|
7.
|
M40
|
40
|
|
8.
|
M45
|
45
|
|
9.
|
M50
|
50
|
|
10.
|
M55
|
55
|
NOTE - The above values
correspond to the site control having proper storage of cement; weigh batching of all materials; controlled addition of water,
regular checking of all materials. Aggregate grading and moisture content; and
periodical checking of workability and strength. Where there is deviation from
the above. Values given in the above table shall be increased by 1 N/mm2.
AN EXAMPLE:
When repeated no of samples
gives different results, then we need to know how much widely the readings are
spread. The spread of results tells us something about the uncertainty of a
measurement. By knowing how large this results are spread. We can easily judge
the quality of the measurement or set of measurements.The usual way to quantify
spread is standard deviation. The standard deviation of a set of numbers shows
us the values are how different the individual readings typically are from the
average of the set. Mathematically standard deviation is stated as, the square
root of deviations of all the result. This is denoted by σ.
The Standard deviation will be less if the
quality control at site is good and most of the test results will be
approximately equal to the mean value. If quality control is poor, then the
test results will have much difference from the mean value and therefore, standard deviation will be higher.
Hera this table showing that the calculation of standard deviation for a Set of 30 Concrete Cube Test Results.
| Sample number | Crushing strength(mix let be X)Mpa | Avg strength µ=∑X/n | Deviation(X-µ) | Square of Deviation(X-µ)2 |
1
|
43
|
42.167
|
0.83
|
0.6889
|
2
|
47
|
4.83
|
23.3289
|
|
3
|
49
|
6.83
|
46.6489
|
|
4
|
42
|
-0.167
|
0.027889
|
|
5
|
46
|
3.833
|
14.69189
|
|
6
|
45
|
2.833
|
8.025889
|
|
7
|
44
|
1.833
|
3.359889
|
|
8
|
41
|
-1.167
|
1.361889
|
|
9
|
40
|
-2.167
|
4.695889
|
|
10
|
38
|
-4.167
|
17.36389
|
|
11
|
37
|
-5.167
|
26.69789
|
|
12
|
39
|
-3.167
|
10.02989
|
|
13
|
35
|
-7.167
|
51.36589
|
|
14
|
36
|
-6.167
|
38.03189
|
|
15
|
48
|
5.83
|
33.9889
|
|
16
|
46
|
3.83
|
14.6689
|
|
17
|
47
|
4.83
|
23.3289
|
|
18
|
40
|
-2.167
|
4.695889
|
|
19
|
38
|
-4.167
|
17.36389
|
|
20
|
48
|
5.83
|
33.9889
|
|
21
|
43
|
0.83
|
0.6889
|
|
22
|
45
|
2.83
|
8.0089
|
|
23
|
44
|
1.83
|
3.3489
|
|
24
|
47
|
4.83
|
23.3289
|
|
25
|
37
|
-5.167
|
26.69789
|
|
26
|
39
|
-3.167
|
10.02989
|
|
27
|
36
|
-6.167
|
38.03189
|
|
28
|
42
|
-0.167
|
0.027889
|
|
29
|
43
|
0.83
|
0.6889
|
|
30
|
40
|
-2.167
|
4.695889
|
|
| Total=1265 | Total=489.9028 |
Standard deviation = √[489.9/ (n-1)] = √(489.9/29) = 4.11 MPa
Where, n = Total number of samples
Coefficient of Variation = (Standard deviation/Average strength)*100
= (4.11/42.167)*100
= 9.79
If we consider less no. of samples that will
increase standard deviation i.e. if we consider 20 samples then SD is 4.34 more
in the no of samples means accurate in the SD



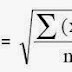






shared article is helpful but can you share the details how to plot the distribution graph as you shown above with mean+3,2,1,mean , Mean-1,-2,-3...... please reply
ReplyDeleteActually the graph was showing the mean +ve to -ve and that showing the values of mean with respect to the data%.if the % of data 99% then the mean will be plus or minus 3.
DeleteInformative post you posted.
ReplyDeleteHi Guys, Please visit my Website and give me Suggestion.
www.accrotech-testequipments.com
Nice Blog !! I was looking for blogs related of Concrete Testing Equipment Supplier . Then i found this blog, this is really nice and interested to read. Thanks to author for sharing this type of information.
ReplyDeleteThanks for sharing this useful information. I am collecting more details about Concrete Testing Equipment Manufacturer If you have relevant data then kindly keep sharing.
ReplyDeleteI wonder if you could use the same technique to build, say, a wall?ready mix concrete
ReplyDeleteA well explanation about Standard Deviation of Concrete Cube Test
ReplyDeleteThanq for giving us information about standard deviation.
ReplyDeleteStandard deviation value for M30 to M55 is 5
ReplyDeleteThe values mentioned in this post are assumed they mentioned above the table and for exact values we need to follow the procedures as mentioned in example
Deletewww.concretetech.net
ReplyDeleteThank you for information.
ReplyDeleteWhich value deduction of RCC not applicable
ReplyDelete